主页
归档
朋友
关于

题解 CF1286C Madhouse

这个 0.7770.777 让我想起了某位 EDG 的退役打野选手

—— Sooke

4396（无 端 迫 害）

我们首先考虑如果我们询问了一段区间 [1,n][1 ,n ] ，我们可以得到什么信息。

我们考虑把 s1,s2,s3⋯sns_1 , s_{2} , s_{3} \cdots s_n 在每种长度的子串中出现的次数给写出来（以 n=5n = 5 时的情况为例）。

lenlen s1s_1 s2s_2 s3s_3 s4s_4 s5s_5
1 1 1 1 1 1
2 1 2 2 2 1
3 1 2 3 2 1

看出规律了吗？如果看不出来的话，我们把每列的数做差分之后的结果再写出来。

lenlen s1s_1 s2s_2 s3s_3 s4s_4 s5s_5
1 1 1 1 1 1
2 0 1 1 1 0
3 0 0 1 0 0

这样以来，我们是不是可以得到 s[l+r2]s[\frac{l + r}2] 的值（当 lenlen 为奇数的时候才可以），并且可以得到 ⌊len2⌋\lfloor \frac {len}2 \rfloor 组形如 「sxs_x 和 sys_y 分别是 aa 和 bb 」（其中 aa 和 bb 代表两个字符）的限制。

我们接下来考虑如何利用这个性质来解决这道题目。

考虑将这个字符串划分为三段，分别为 [1,s][1 , s]，[s+1,t][s + 1, t]，[t+1,n][t + 1, n] 三段区间。

这个分法要满足一定的要求，具体是什么要求稍后会讲到。

然后询问 [1,t][1 , t] ，[s+1,n][s + 1 , n] ，[s+1,n−1][s + 1, n - 1] 三段。

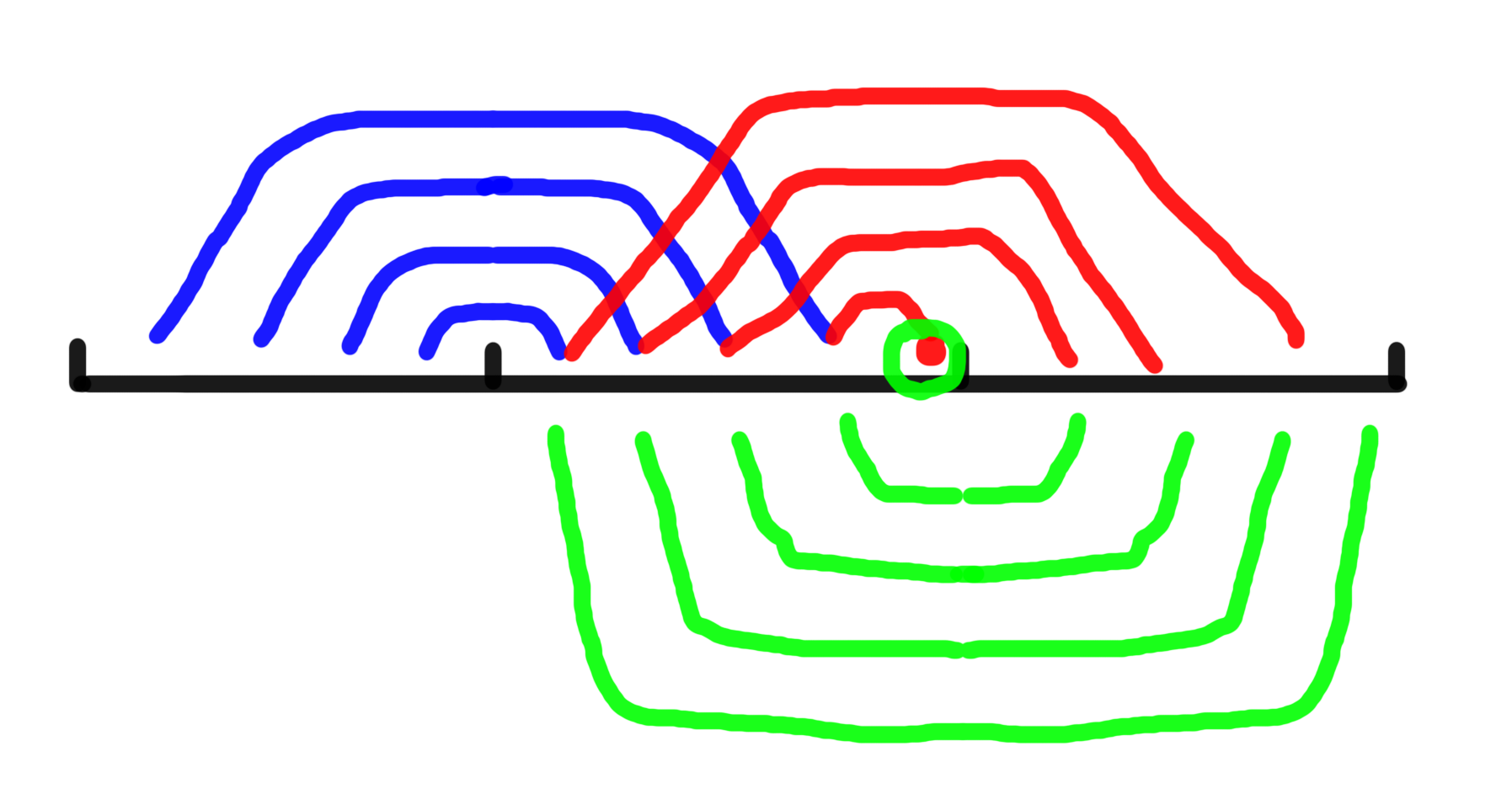
把每组得到的约束条件都连起来，我们可以得到一个差不多长成这样的图……

注意那个画着一个绿色圈圈的位置，我们假设我们已经知道这里是什么。

那么考虑交替通过绿色和红色的约束就可以知道第二段和第三段，然后通过蓝色的约束就可以知道第一段了。

那么只要在询问 [s+1,n][s + 1 , n] 的时候那个长度为奇数的时候中间可以直接知道的数落在它身上就可以了。

这样一来，我们就知道这个分法要满足什么要求了。

我们设三段的长度分别为 len1,len2,len3len1 , len2 , len3，那么需要满足：

  • len2+len3len2 + len3 为奇数
  • len2>len3len2 > len3
  • len2>len1len2 > len1 （否则无法由第二段推出完整的 len1len1）

可以通过对 nmod  3n \mod 3 进行分类讨论得出 len1,len2,len3len1 , len2 , len3 。

每次询问的长度都是 23n\frac 23 n 级别，询问出来的字串数量都是 29n2\frac 29 n^2 级别，最终三次询问加起来就大约是 23n2≈0.66666n2<0.777n2\frac 23 n^2 \approx 0.66666 n^2 < 0.777 n^2 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
#include<bits/stdc++.h>

#define ll long long
#define INF 2147483647

int inp(){
    char c = getchar();
    int neg = 1;
    while(c < '0' || c > '9'){
        if(c == '-')
            neg = -1;
        c = getchar();
    }
    int sum = 0;
    while(c >= '0' && c <= '9'){
        sum = sum * 10 + c - '0';
        c = getchar();
    }
    return sum * neg;
}

char ans[110], s[110];
char f[110][110][2];

char _query(int x){
    std::cout << "? " << x << ' ' << x << std::endl;
    char c = getchar();
    while(c < 'a' || c > 'z')
        c = getchar();
    return c;
}

std::vector<std::string> vec[110];
std::string str;

bool cmp(std::string a, std::string b){
    return a.size() < b.size();
}

int cnt[30], q[110], cou[30];
int qf = 1, qe = 0, n;
bool used[110], have[110][110];
int last[30], delta[30];

void query(int l, int r){
    for(int i = 1; i <= r - l + 1; i++)
        vec[i].clear();
    std::cout << "? " << l << ' ' << r << std::endl;
    for(int i = 1; i <= ((r - l + 1) * (r - l + 2) >> 1); i++){
        std::cin >> str;
        vec[(int)(str.size())].push_back(str);
        // printf("str.size() = %d\n", (int)(str.size()));
    }
    memset(delta, 0, sizeof(delta));
    memset(last, 0, sizeof(last));
    for(int i = 0; i < (int)(vec[1].size()); i++){
        last[vec[1][i][0] - 'a']++;
        delta[vec[1][i][0] - 'a']++;
    }
    for(int i = 2; i <= ((r - l) >> 1) + 1; i++){
        memset(cnt, 0, sizeof(cnt));
        for(int j = 0; j < (int)(vec[i].size()); j++)
            for(int u = 0; u < i; u++)
                cnt[vec[i][j][u] - 'a']++;
        int cur = 0;
        // printf("i = %d\n", i);
        for(int j = 0; j < 26; j++){
            cnt[j] -= last[j];
            last[j] += cnt[j];
            int last = cnt[j];
            while(cnt[j] < delta[j]){
                // printf("link %d %d\n", l + i - 2, r - i + 2);
                f[l + i - 2][r - i + 2][cur] = 'a' + j;
                f[r - i + 2][l + i - 2][cur] = 'a' + j;
                have[l + i - 2][r - i + 2] = true;
                have[r - i + 2][l + i - 2] = true;
                cur++;
                cnt[j]++;
            }
            delta[j] = last;
        }
    }
    // printf("maxinum %d | %d ", ((r - l + 1) >> 1) + ((r - l) & 1), vec[2].size());
    int mid = (l + r) >> 1;
    if((r - l + 1) & 1){
        for(int i = 0; i < 26; i++)
            if(delta[i] && !used[mid]){
                used[mid] = true;
                ans[mid] = 'a' + i;
                q[++qe] = mid;
                // printf("ans[%d] = '%c' | %d\n", mid, 'a' + i, cnt[i]);
            }
    } else {
        int cur = 0;
        for(int i = 0; i < 26; i++)
            while(delta[i]){
                int mid = (l + r) >> 1;
                // printf("| link %d %d | %d left\n", mid, mid + 1, delta[i]);
                f[mid][mid + 1][cur] = 'a' + i;
                f[mid + 1][mid][cur] = 'a' + i;
                have[mid][mid + 1] = true;
                have[mid + 1][mid] = true;
                cur++;
                delta[i]--;
            }
    }
}

void print(int len){
    printf("! ");
    for(int i = 1; i <= len; i++)
        putchar(ans[i]);
    std::cout << std::endl;
}

void bfs(){
    while(qf <= qe){
        int i = q[qf++];
        for(int j = 1; j <= n; j++)
            if(have[i][j] && !used[j]){
                ans[j] = f[i][j][f[i][j][0] == ans[i]];
                used[j] = true;
                q[++qe] = j;
            }
    }
}

int main(){
    n = inp();
    if(n <= 3){
        for(int i = 1; i <= n; i++)
            ans[i] = _query(i);
        print(n);
        return 0;
    }
    int len1 = (n / 3);
    int len2 = len1, len3 = len1;
    if(n % 3 == 0){
        len2++;
        len3--;
    } else if(n % 3 == 1){
        len2++;
    } else {
        len2++;
        len3++;
    }
    query(1, len1 + len2);
    query(len1 + 1, n);
    query(len1 + 1, n - 1);
    // for(int i = 1; i <= n; i++)
    //     for(int j = 1; j <= n; j++)
    //         if(have[i][j])
    //             printf("{%d, %d} {%c, %c}\n", i, j, f[i][j][0], f[i][j][1]);
    bfs();
    print(n);
}

QQ

|

Codeforces

|

Luogu

|

Github
本站由 Hexo 驱动，使用 Azurus 作为主题。